newsletter of the ACM Special Interest Group on Genetic and Evolutionary Computation

Table of Contents
Editorial
Welcome to the 4th (Winter) 2022 issue of the SIGEvolution newsletter! We start with an overview of the 2022 Genetic and Evolutionary Conference GECCO, celebrated in Boston from July 9th-13th, 2022 as the first-ever hybrid GECCO. We continue with a summary of a recent article using low-dimensional Euclidean embedding to generate striking visualizations of combinatorial search spaces. The third article overviews a recent PhD dissertation on the use of genetic programming hyper-heuristics in the context of many-objectives job-shop scheduling. We complete the issue with recent announcements and call for submissions. Please get in touch if you would like to contribute an article for a future issue or have suggestions for the newsletter.
GECCO 2022: Summary and Statistics
Jonathan Fieldsend, University of Exeter, United Kingdom
Markus Wagner, University of Adelaide, Australia
The 2022 Genetic and Evolutionary Computation Conference (GECCO 2022) took place in Boston, on July 9th-13th, 2022, as the first-ever “hybrid” GECCO. Hybrid here meant that about half of the attendees were physically present in Boston, while the others joined online. In the following, we provide statistics about submissions and authorship, and some comments about the evolution and growth of GECCO.
GECCO 2022 would not have been possible without the enormous team of helpers: 32 organisers, 26 track chairs, dozens of A/V (audio-video) volunteers, the reviewers, … and so many more. We thank everyone for contributing to the efforts of this community event.
GECCO 2022 was organized into these 13 main tracks: Ant Colony Optimization and Swarm Intelligence (ACO-SI), Complex Systems (Artificial Life/Artificial Immune Systems/ Generative and Developmental Systems/Evolutionary Robotics/Evolvable Hardware) (CS), Evolutionary Combinatorial Optimization and Metaheuristics (ECOM), Evolutionary Machine Learning (EML), Evolutionary Multiobjective Optimization (EMO), Evolutionary Numerical Optimization (ENUM), Genetic Algorithms (GA), General Evolutionary Computation and Hybrids (GECH), Genetic Programming (GP), Neuroevolution (NE), Real World Applications (RWA), Search-Based Software Engineering (SBSE) and Theory.
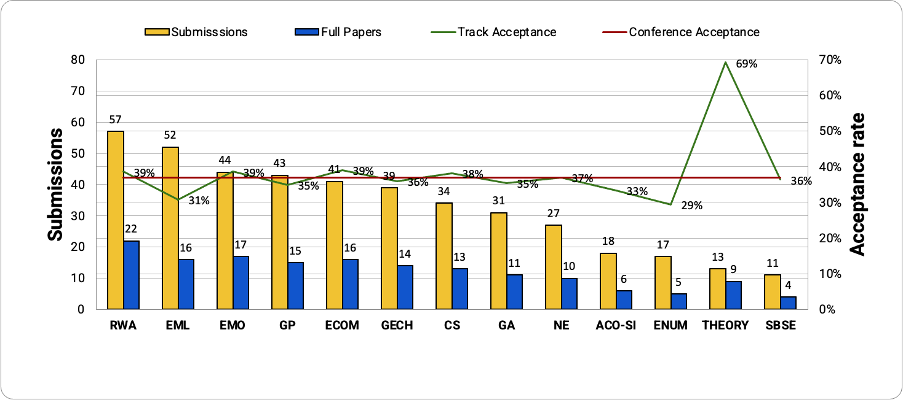
The number of submissions (yellow), the number of accepted full papers (blue), the acceptance rate of each track (green) and the acceptance rate of the conference (red) are shown in Fig 1. The tracks are sorted by the number of full paper submissions they received (decreasing from left to right). The RWA track received the largest number of submissions. The acceptance rate is different in each track, with slight deviations around the average in most of the cases. In the case of the tracks with fewer submissions, Theory and SBSE, these deviations are high because one paper more or less, here, gives a large change in the acceptance rate. The largest acceptance rate was 69% in the Theory track, while the lowest acceptance rate was 29% in the ENUM track (though in the latter case this largely stemmed from a track change for a paper after review in consultation with track chairs and authors).
The submissions received by the main tracks at GECCO 2022 were authored by 973 researchers from 49 countries with 80% of authors affiliated with just 15 countries (see Fig. 2). The USA, the hosting country, returned to the top spot this year with 135 authors (slightly under 14% of the total). China is in the second position with 106 authors, then Germany (92) followed by France (85) – the host in 2021.
In addition to the submissions to the main conference, GECCO 2022 received 131 papers for 22 specialized workshops, 9 submissions to the Student Workshop, 21 Late-Breaking Abstracts and 24 Hot Off the Press submissions. GECCO 2022 also provided 38 tutorials (introductory, advanced and specialized) from among 39 proposals. This edition of GECCO was very fortunate to have three fantastic keynote speakers: Cynthia Breazeal (Massachusetts Institute of Technology, USA), Erik Goodman (Michigan State University, USA), and Meinolf Sellmann (InsideOpt, USA)

Historical evolution of GECCO
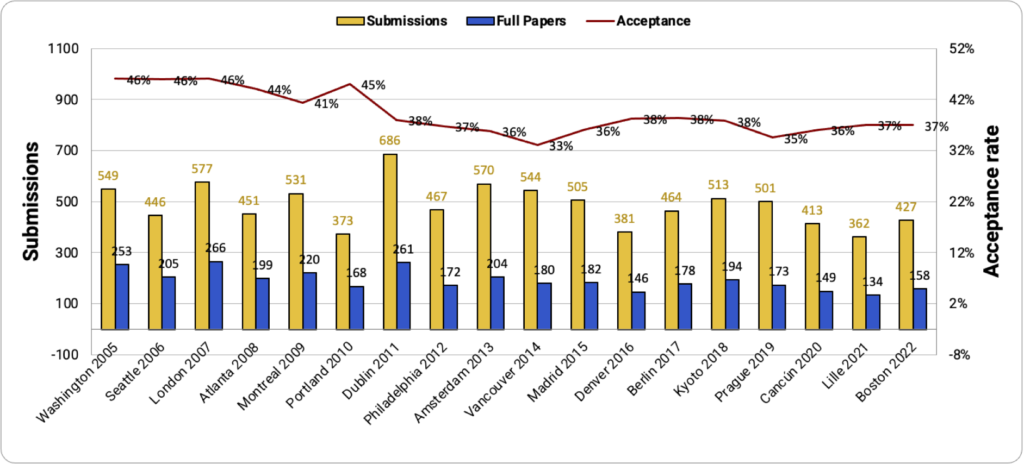
Fig. 4 compares the number of submissions and acceptance rate of GECCO 2022 to its previous editions. There has been a degree of bounce back since the onset of the COVID-19 pandemic, and although the total number of submissions is the fourth lowest since 2005, it is not far away from the average for North American versions of GECCO. The acceptance rate of GECCO 2022 is below 40%, the same as in the last 10 years, which has been in the range of 33% to 38%. Although the number of submissions is on the lower side, the number of participants in the first hybrid GECCO is the highest of any GECCO, which bodes well for future editions (see below).
The evolution of the main GECCO tracks is shown in Fig. 5, where the (vertical) width of each line is relative to the size of the track (number of accepted full papers) and the vertical position of the line gives the relative order (larger to smaller, from top to bottom).

Finally, the growth of GECCO is also clearly illustrated by the number of registrations, which achieved a historical maximum of 987 in GECCO 2022. The record of registrations for an onsite edition is 691, reached in GECCO 2018 (Kyoto, Japan); the record of registration for an online edition is 946, reached in GECCO 2021. For online participation, offering reduced registration fees for non-presenters contributed to having attendees that do not usually go to GECCO, and it helped to achieve visibility of the conference around the globe. All attendees can still watch some of the pre-recorded videos of the talks, keynotes, and plenary sessions, and participate in the discussion chats for at least the next few months.

Impacted by COVID-19, GECCO 2022 relied on established tools to provide networking and socialization among the attendees in the online mode, and between the participants in the two modes. Gather and Whova played that role. While we all miss sitting at a real table with some drinks to discuss research ideas, Gather tried to fill that gap by providing virtual tables, rooms, whiteboards, and a “cam-to-cam” interface.
We hope attendees enjoyed these tools and felt a bit closer during the conference – they have, for sure, used it a lot: 35 jobs were posted, 67 photos were shared, about 142 days of content was watched, and each was streamed by about 150 attendees, and over 8000 messages were sent.
Another aspect that was particularly important this year was that of sustainability – not only did we aim to provide an inclusive event that allowed for remote participation (while considering time zones, to the extent possible), but also one that considers the planet that we live on. Among other things, mugs and glasses were provided during the official breaks, the beer at the social event was local, the proceedings have not been printed, the signage at the hotel was electronic, we distributed the GECCO 2020 coffee mugs, and the three keynote speakers were locally sourced, too. What has been the impact of this, or to put differently, how much CO2 did we save? This isn’t easy to grasp, but as an example: for one round-trip Rome-Boston, 100 trees need to grow for 1 year… and we had about 500 online attendees.
Lastly, let us wrap up this report with one more number: 584. This is the number of private group chats that were set up in Whova – no, we cannot see what has been discussed 🙂. We would also like to think that new research ideas have sparked, not only in Boston but spanning the globe… and some of these ideas, we might see in about half a year’s time at GECCO 2023.
Visualizing Combinatorial Search Spaces with Low-Dimensional Euclidean Embedding
Krzysztof Michalak, Department of Information Technologies, Wroclaw University of Economics and Business, Poland
Abstract
The low dimensional Euclidean embedding method (LDEE) allows visualizing combinatorial search spaces by mapping to the Euclidean space ℝk (with k = 2 or 3 in practice). The mapping of a combinatorial search space Ω to ℝk is obtained by first running the t‑SNE (t-distributed stochastic neighbor embedding) algorithm with an appropriate probability distribution used for the space Ω (for example the Mallows distribution for permutation spaces). Subsequently, the vacuum embedding algorithm, proposed in this article, is used in order to ensure good visual separation of solutions in ℝk. The LDEE method maps solutions to a regular grid in ℝk, which can be used for plotting various kinds of information. Apart from solution evaluations or comparisons of multiple objectives, the proposed method can be used for analyzing the behavior of the population in population-based metaheuristics, the working of genetic operators, etc. This newsletter contribution summarizes a recent research article [1].
Overview of the LDEE Method
The low dimensional Euclidean embedding method (LDEE) maps solutions in a 1-1 manner from a combinatorial search space Ω to coordinates in the Euclidean space ℝk. The attributes of solutions, such as the values of the objectives, constraints or any other parameters of the solutions are not transformed by LDEE and can be used for plotting using the regular layout of points in ℝk as the basis for the plots. The method consists of two main steps: t-SNE and vacuum embedding.
The t-SNE Algorithm
The t-SNE (t-distributed stochastic neighbor embedding) algorithm is a well-known dimensionality reduction method, which maps points from the source space X into the target space Y. Distances in the source space X are converted into conditional probabilities that represent similarities between points, and points in the target space Y are iteratively moved in order to minimize the Kullback‑Leibler divergence between the distributions of distances in the source and target spaces. In machine learning applications, the source space X is usually Euclidean with the Gaussian distribution of the distances, however, as shown in this article, the underlying assumptions of the t-SNE method hold as well if the source space X is a permutation space with the Mallows model. For other combinatorial search spaces, other distances can be used, such as the Hamming distance for the space of binary vectors. Fig. 1 shows the working of the t-SNE method mapping solutions of the four-peaks problem (4PP) from {0, 1}100 to ℝ2. As the figure shows, some separation is obtained in ℝ2, but the points do not form a regular grid.

The Vacuum Embedding Algorithm
The vacuum embedding algorithm proposed in the original article [1] is used for spreading the points more evenly on a rectangular grid. It is inspired by the behavior of particles of air which expand in an empty space filling it evenly. In the calculations, empty spaces “attract” solutions, which thereby expand until a large portion of the available space is filled. After a predetermined number of iterations, a “snapping” mechanism can be activated, which places the points exactly at the grid points. Fig. 2 presents the fitting of the points to a square grid by the VE method working on solutions of the 4PP with the length of the binary vectors equal to n = 100.

Fig. 2. Fitting of the points to a square grid by the vacuum embedding method working on solutions of the 4PP with n = 100. Top row: on the left is the embedding produced by t-SNE (from which the VE starts) and in the middle and on the right the embedding produced after 20 and 50 iterations of the VE. Middle row: VE iterations before edge snapping became active: 100, 200, and 500. Bottom row: VE iterations in which edge snapping was active: 501, 530, and the last one 581.
Applications
Because the proposed method maps solutions from a combinatorial search space Ω to the Euclidean space ℝk, multiple visualization methods can be used to present various aspects of the search space or the population processed by a population-based metaheuristic, such as an evolutionary algorithm.
Analyzing Search Spaces
Visualizing solutions found by an evolutionary algorithm can show some interesting characteristics of the search space of the problem. Fig. 3 shows solutions found by an evolutionary algorithm solving the four-peaks Problem with n = 100 and T = 15. In this problem, a solution x ∈ {0, 1}100 is evaluated as follows. Let o(x) be the number of contiguous ones starting at position 1 in the genotype and z(x) the number of contiguous zeros ending at position 100 in the genotype. A REWARD is set to 100 if both o(x) > T and z(x) > T. For n = 100 and T = 15, the optimum is reached by two vectors in {0, 1}100: a vector of 84 ones followed by 16 zeros and a vector of 16 ones followed by 84 zeros. In Fig. 3 a plateau of REWARDed solutions is clearly visible. Also, it is apparent, that there exist solutions very similar to others, but with much lower evaluation (dark-blue dots) in which a contiguous sequence of zeros or ones has been interrupted by the opposite values.

Fig. 3. Solutions found by an evolutionary algorithm solving the Four Peaks Problem. A plateau of REWARDed solutions is clearly visible.
Comparing search spaces of different optimization problems can also provide some interesting insights. Fig. 4 shows a comparison of search spaces of the Firefighter Problem (FFP), the Knapsack Problem (KP), the Quadratic Assignment Problem (QAP), and the Travelling Salesman Problem (TSP). Except for the KP, these are minimization problems, which is reflected by the proportion of the search space consisting of solutions found by the evolutionary algorithm, which have low values of the objective function (high values of the objective function for the KP, correspondingly). The FFP, QAP, and TSP are defined on the permutation space, while the search space for the KP is the space of binary vectors. It is easy to see that the QAP turned out to be the hardest to solve because lots of solutions found by the optimizer have high objective function values. Naturally, the difficulty of the problem instance depends on the parameters of the instance, as shown below in the analysis of the FFP search spaces.

The LDEE method can be used for comparing the search spaces of the same optimization problem with varying parameters. Naturally, setting different values of the parameters can dramatically change the difficulty of the problem instances. Fig. 5 shows search spaces of the firefighter problem (FFP) obtained for different parameterizations of the problem with the color corresponding to the number of burnt graph nodes (to be minimized). In the case of the FFP, the Nf parameter (interpreted as “the number of firefighters”) determines the number of nodes in the graph which can become defended in each time step. Naturally, having more firefighters (higher Nf value) translates to easier graph defence. Fig. 5 shows a comparison of the search spaces for the FFP with |V| = 1000 graph nodes and varying values of Nf. It can be concluded that:
- With a small number of firefighters (Nf = 2), defending the graph is difficult (lots of solutions with a high number of burnt vertices are present), but some solutions work remarkably well (blue areas)
- With a large number of firefighters (Nf = 40), not only defending the graph is easy (lots of solutions with a low number of burnt vertices are present), but also many similar solutions work similarly well (large areas with the same color). This can be explained by the fact, that with many firefighters, many permutations actually represent the same course of action (protecting the same graph nodes in the same time step).
- There is a very interesting change in the difficulty of the problem between Nf = 10 and Nf = 20. Even though the range in which the number of graph nodes lost to the fire varies is similar for Nf = 10, Nf = 15, and Nf = 20, the proportion of good solutions differs a lot. For Nf = 10 it is relatively hard to find good solutions, and for Nf = 20 it is much easier. Also, the presence of large dark-blue areas for Nf = 20 suggests, that with that number of firefighters, there are many permutations which translate to equally good solutions (nodes of the graph can be protected in various order and the graph can still survive). A completely different situation can be observed for Nf = 10, for which a good solution has to represent a carefully chosen selection of nodes to protect, as evidenced by only a few dark-blue areas.

Population Dynamics
LDEE-based visualizations can be used for analyzing the dynamics of the population. For example, Fig. 6 presents population dynamics in one run of the evolutionary algorithm solving the firefighter problem with |V| = 1000 graph nodes and Nf = 15. Solutions are plotted as white dots on a background representing solution evaluations from 30 runs of the evolutionary algorithm. In generation 73, a mutated solution can be seen exploring a new area characterized by low solution evaluations (dark blue). This mutated solution does not seem to be enough to drive the entire population to that region, but in generation 77 another mutated solution appears and soon the entire population starts exploring the new area (generations 81-88). In some other runs, subpopulations could be observed (Fig. 7). Using various attributes of the plotted markers it is possible to visualize an entire run of an evolutionary algorithm or even several runs in one plot.


Fig. 7. Subpopulations forming in one of the EA runs solving the firefighter problem with |V| = 1000 graph nodes and Nf = 15 (top-right corner). Solutions are plotted as white dots on a background representing solution evaluations from 30 runs of the evolutionary algorithm.
Other Applications
The LDEE method can be used for visualizing other aspects of optimization algorithms as well, such as multiple properties of solutions and the working of genetic operators. For the discussion of these applications, readers are referred to the original article [1] and LDEE method website.
Conclusion
The Low Dimensional Euclidean Embedding Method (LDEE) allows visualizing combinatorial search spaces by mapping to the Euclidean space ℝk (with k = 2 or 3 in practice). The transformation is obtained by performing the t-SNE mapping using an appropriate probability distribution in the combinatorial search space (such as the Mallows distribution for permutation spaces) followed by a vacuum embedding (VE) step which places the points more uniformly on a rectangular grid. A perfect grid arrangement can be achieved by applying an “edge snapping” mechanism in the last part of the VE run. It should be noted, however, that later steps are optional and can be applied as needed, so t-SNE, t-SNE + VE, and t-SNE + VE + “edge snapping” can be used if needed. The square layout produced by the LDEE can be used for visualizing search spaces, population dynamics and working of genetic operators using a variety of 2-d and 3-d plots.
Acknowledgements
This work was supported by the Wrocław Centre for Networking and Supercomputing (http://wcss.pl) under Grant 407.
Additional Information
Additional information about the LDEE method and tools for applying the method to any dataset are available at http://krzysztof-michalak.pl/research/ldee/index.html
References
[1] K. Michalak, “Low-Dimensional Euclidean Embedding for Visualization of Search Spaces in Combinatorial Optimization,” in IEEE Transactions on Evolutionary Computation, vol. 23, no. 2, pp. 232-246, April 2019, doi: 10.1109/TEVC.2018.2846636.
Many-Objective Genetic Programming for Job-Shop Scheduling
Atiya Masood (masood.atiy@ecs.vuw.ac.nz), Victoria University of Wellington, Wellington, New Zealand
Introduction
This article overviews a recent PhD dissertation representing the first effort at many-objective optimization in job shop scheduling (JSS). The thesis develops genetic programming hyperheuristic (GP-HH) approaches to evolve effective dispatching rules for many conflicting objectives in JSS problems. The aim is to develop GP-HH methods that alleviate issues related to many-objective optimization in JSS problems and evolve new effective dispatching rules capable of enhancing job shops’ productivity.
Background
Job shop scheduling (JSS) [7] is a non-deterministic polynomial-time (NP) hard combinatorial optimization problem that involves assigning different manufacturing jobs to machines at specific times while trying to minimize a number of objectives, including the mean flowtime (mF), maximal flowtime (maxF), mean weighted tardiness (mWT) and maximal weighted tardiness (maxWT). These objectives are also considered to minimize in this thesis. JSS problems have drawn a lot of interest from academics and industry experts. As reported by Johns and Rabelo [5], thousands of manufacturers contribute billions of dollars to the United State’s economy. Furthermore, JSS is considered one of the significant production scheduling problems in practice. It has a wide range of applications in many industries such as cloud computing [8] and management and operations research [6]. JSS has received substantial research attention due to its high computational challenges and strong practical value. A JSS problem usually has a set of machines on the shop floor that can be used to process a set of jobs [7]. Each job has a predetermined sequence of operations, which needs to be carried out in order to complete the job. An example of a job shop studied in this thesis is shown in Fig 1.

Dispatching rules have been applied extensively to JSS problems due to their computational efficiency. Dispatching rules can be seen as a priority function which is used to assign priority to each job waiting to be processed by a machine. Then, the next job to process will be selected based on the priority value. Such computation is carried out at each decision point (e.g., when a machine becomes idle) and can be done efficiently. This can be seen in Fig 2.

Genetic Programming (GP) has been a promising approach for designing dispatching rule heuristics automatically because GP has an ability to evolve priority functions with its flexible representation.The hyper-heuristic approach that uses GP to solve JSS problems is known as GP based Hyper-Heuristic (GP- HH ) [1]. This thesis evolves dispatching rules for both static and dynamic JSS problems automatically.
Many-objective optimization has become an active research topic [2]. As emphasized by Deb in [2], a large proportion of real-world problems can be described naturally as many-objective problems (MaOPs). A class of optimization problems with more than three objectives is referred to as many-objective optimization. The last decade has witnessed the emergence of many-objective optimization as a booming topic in a wide range of complex modern real-world scenarios.
Scheduling theory has been established over the years. Still, most existing literature on the automatic design of dispatching rules mainly concentrates on single-objective JSS [3] and multi-objective JSS [4].
Only a few algorithms in the literature tackle JSS problems with more than three scheduling objectives. These algorithms utilize the conventional MOEAs (NSGA-II and SPEA2), but MOEAs experienced substantial difficulties when they were adopted to tackle MaOPs [2]. It is both theoretically and practically important to develop innovative GP-HH algorithms for many-objective JSS.
Objectives
This research was broken down into the following key objectives:
- Investigate how GP can be used to handle many-objective JSS problems.
- Investigate how to develop GP-HH approaches for the non-uniform Pareto front of many-objective JSS problems which can evolve high-quality Pareto-optimal dispatching rules.
- Investigate how to hybridize a local search with a global search and improve the quality of the evolved rules in many-objective JSS.
Contributions
The main contributions of this thesis are to propose:
- The first many-objective GP-HH method for JSS problems to find the Pareto-fronts of non-dominated dispatching rules. In order to visualize the interdependencies between different objectives, this thesis used the aggregated Pareto-front. Part of this contribution has been published at:
- A. Masood, Y. Mei, G. Chen, and M. Zhang, Many-objective genetic programming for job-shop scheduling. IEEE Congress on Evolutionary Computation (CEC 2016)
- Two adaptive reference point approaches (model-free and model-driven). In both approaches, the reference points are generated according to the distribution of the evolved dispatching rules. Part of this contribution has been published at:
- A. Masood, Chen, G., and Zhang, M. Genetic Programming Hyper-heuristic with Gaussian Process-based Reference Point Adaption for Many-Objective Job Shop Scheduling. IEEE Congress on Evolutionary Computation (CEC 2022).
- The first algorithm that combines GP as a global search with Pareto Local Search (PLS) as a local search in many-objective JSS. Part of this contribution has been published at:
- A. Masood, G. Chen,Y. Mei, H. Al-Sahaf, and M. Zhang. A Fitness-based selection method for Genetic Programming with Pareto Local Search in Many-Objective Job Shop Scheduling. IEEE Congress on Evolutionary Computation (CEC 2020)
Additional Resources
This thesis is available on the Victoria University of Wellington database:
Many-Objective Genetic Programming for Job-Shop Scheduling
References
- Branke, J., Nguyen, S., Pickardt, C., Zhang, M.: Automated Design of Production Scheduling Heuristics: A Review. IEEE Trans. Evolutionary Computation 20(1), 110–124 (2016)
- Deb, K., Jain, H.: An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation 18(4), 577–601 (2014)
- Hildebrandt, T., Heger, J., Scholz-Reiter, B.: Towards improved dispatching rules for complex shop floor scenarios: A genetic programming approach. In: Proceedings of Genetic and Evolutionary Computation Conference. pp. 257–264. ACM (2010)
- Ishibuchi, H., Murata, T.: A multi-objective genetic local search algorithm and its application to flowshop scheduling. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 28(3), 392–403 (1998)
- Jones, A., Rabelo, L.C., Sharawi, A.T.: Survey of job shop scheduling techniques. Wiley encyclopedia of electrical and electronics engineering (2001)
- Leung, J.Y.T. (ed.): Handbook of Scheduling – Algorithms, Models, and Performance Analysis. Chapman and Hall/CRC (2004)
- Pinedo, M.L.: Scheduling: theory, algorithms, and systems. Springer Science & Business Media (2012)
- Tsai, C.W., Rodrigues, J.J.P.C.: Metaheuristic Scheduling for Cloud: A Survey. IEEE Systems Journal 8(1), 279–291 (2014)
Announcements

Evolutionary Computation Tool-kit in Python
Moshe Sipper, Ben-Gurion University of the Negev, Israel
EC-KitY is a comprehensive Python library for doing evolutionary computation (EC), licensed under GNU General Public License v3.0, and compatible with scikit-learn. Designed with modern software engineering and machine learning integration in mind, EC-KitY can support all popular EC paradigms, including genetic algorithms, genetic programming, coevolution, evolutionary multi-objective optimization, and more. EC-KitY is:
- A comprehensive toolkit for running evolutionary algorithms
- Written in Python
- Can work with or without scikit-learn, i.e., supports both sklearn and non-sklearn modes
- Designed with modern software engineering in mind
- Designed to support all popular EC paradigms (GA, GP, ES, coevolution, multi-objective, etc.)
The full description can be found at https://github.com/ec-kity/ec kity/ (or https://www.eckity.org/). There is also a paper: https://arxiv.org/abs/2207.10367
Call for Submissions

GECCO 2023 @ Lisbon (hybrid)
The Genetic and Evolutionary Computation Conference
July 15 – 19, 2003
The Genetic and Evolutionary Computation Conference (GECCO) presents the latest high-quality results in genetic and evolutionary computation since 1999. Topics include: genetic algorithms, genetic programming, ant colony optimization and swarm intelligence, complex systems, evolutionary combinatorial optimization and metaheuristics, evolutionary machine learning, evolutionary multiobjective optimization, evolutionary numerical optimization, neuroevolution, real world applications, search-based software engineering, theory, hybrids and more.
Important Dates
Full papers and poster-only papers deadlines
- Abstract: February 3, 2023
- Submission: February 10, 2023
- Notification: March 31, 2023
- Camera-ready: April 20, 2023

2023 “Humies” Awards for Human-Competitive Results
Produced by Genetic and Evolutionary Computation
Important Dates
- Friday, 2 June 2023: Deadline for entries (consisting of one TEXT file, PDF files for one or more journal or reviewed conference papers, and possible “in press” documentation). Send entries to goodman at msu dot edu
- Friday, 16 June 2023: Finalists will be told by e-mail Friday.
- 30 June 2023: Finalists must submit a 10-minute video presentation to goodman at msu dot edu.
- 15-19 July 2023 (Saturday – Wednesday): GECCO conference.
- Monday, 17 July 2023: Presentation session.
- Wednesday, 19 July 2023: Announcement of awards at plenary session of the GECCO conference.

The 12th International Workshop on Genetic Improvement
Co-located with the 45th IEEE/ACM International Conference on Software Engineering, ICSE 2023, in Melbourne, Australia
We invite submissions that discuss recent develop- ments in all areas of research on, and applications of, Genetic Improvement.
GI is the premier workshop in the field and provides an opportunity for researchers interested in automated program repair and software optimisation to disseminate their work, exchange ideas and discover new research directions.
Important Dates
- Submission Deadline: 13 January 2023 (Fri)
- Notification: 24 February 2023 (Fri)
- Camera-ready: 17 March 2023 (Fri)
- Workshop: TBD May 2023
About this Newsletter
SIGEVOlution is the newsletter of SIGEVO, the ACM Special Interest Group on Genetic and Evolutionary Computation. To join SIGEVO, please follow this link: [WWW].
We solicit contributions in the following categories:
Art: Are you working with Evolutionary Art? We are always looking for nice evolutionary art for the cover page of the newsletter.
Short surveys and position papers. We invite short surveys and position papers in EC and EC-related areas. We are also interested in applications of EC technologies that have solved interesting and important problems.
Software. Are you a developer of a piece of EC software, and wish to tell us about it? Then send us a short summary or a short tutorial of your software.
Lost Gems. Did you read an interesting EC paper that, in your opinion, did not receive enough attention or should be rediscovered? Then send us a page about it.
Dissertations. We invite short summaries, around a page, of theses in EC-related areas that have been recently discussed and are available online.
Meetings Reports. Did you participate in an interesting EC-related event? Would you be willing to tell us about it? Then send us a summary of the event.
Forthcoming Events. If you have an EC event you wish to announce, this is the place.
News and Announcements. Is there anything you wish to announce, such as an employment vacancy? This is the place.
Letters. If you want to ask or to say something to SIGEVO members, please write us a letter!
Suggestions. If you have a suggestion about how to improve the newsletter, please send us an email.
Contributions will be reviewed by members of the newsletter board. We accept contributions in plain text, MS Word, or Latex, but do not forget to send your sources and images.
Enquiries about submissions and contributions can be emailed to gabriela.ochoa@stir.ac.uk
All the issues of SIGEVOlution are also available online at: www.sigevolution.org
Notice to contributing authors to SIG newsletters
As a contributing author, you retain copyright to your article. ACM will refer all requests for republication directly to you.
By submitting your article for distribution in any newsletter of the ACM Special Interest Groups listed below, you hereby grant to ACM the following non-exclusive, perpetual, worldwide rights:
- to publish your work online or in print on condition of acceptance by the editor
- to include the article in the ACM Digital Library and in any Digital Library-related services
- to allow users to make a personal copy of the article for noncommercial, educational, or research purposes
- to upload your video and other supplemental material to the ACM Digital Library, the ACM YouTube channel, and the SIG newsletter site
If third-party materials were used in your published work, supplemental material, or video, that you have the necessary permissions to use those third-party materials in your work
Editor: Gabriela Ochoa
Sub-editor: James McDermott
Associate Editors: Emma Hart, Bill Langdon, Una-May O’Reilly, Nadarajen Veerapen, and Darrell Whitley